1.In ∆ABC right angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C
Solution: 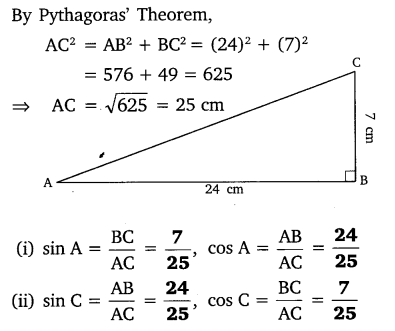
2.In given figure, find tan P – cot R.
Solution: 
3.If sin A = 34 , calculate cos A and tan A.
Solution: 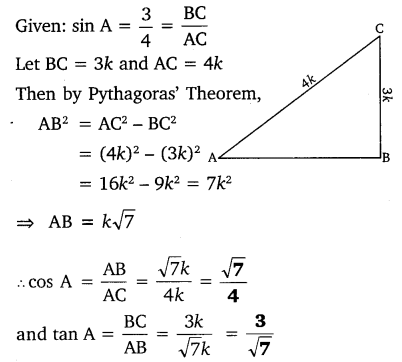
Given 15 cot A = 8, find sin A and sec A.
Solution: 
Given sec θ = 13/12 , calculate all other trigonometric ratios.
Solution: 
6.If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution: 
7.If cot θ = 78, evaluate:
(i) (1+sinθ)(1−sinθ)(1+cosθ)(1−cosθ)
(ii) cot²θ
Solution: 
8.If 3 cot A = 4, check whether 1−tan2A1+tan2A = cos² A – sin² A or not.
Solution: 
9.In triangle ABC, right angled at B, if tan A = 1√3, find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution: 
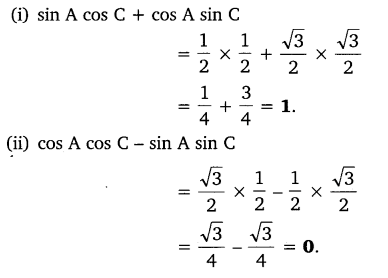
10.In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution: 
11.State whether the following statements are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 125 for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = 43 for some angle.
Solution: 