- Form the pair of linear equations in the following problems, and find their solutions graphically:
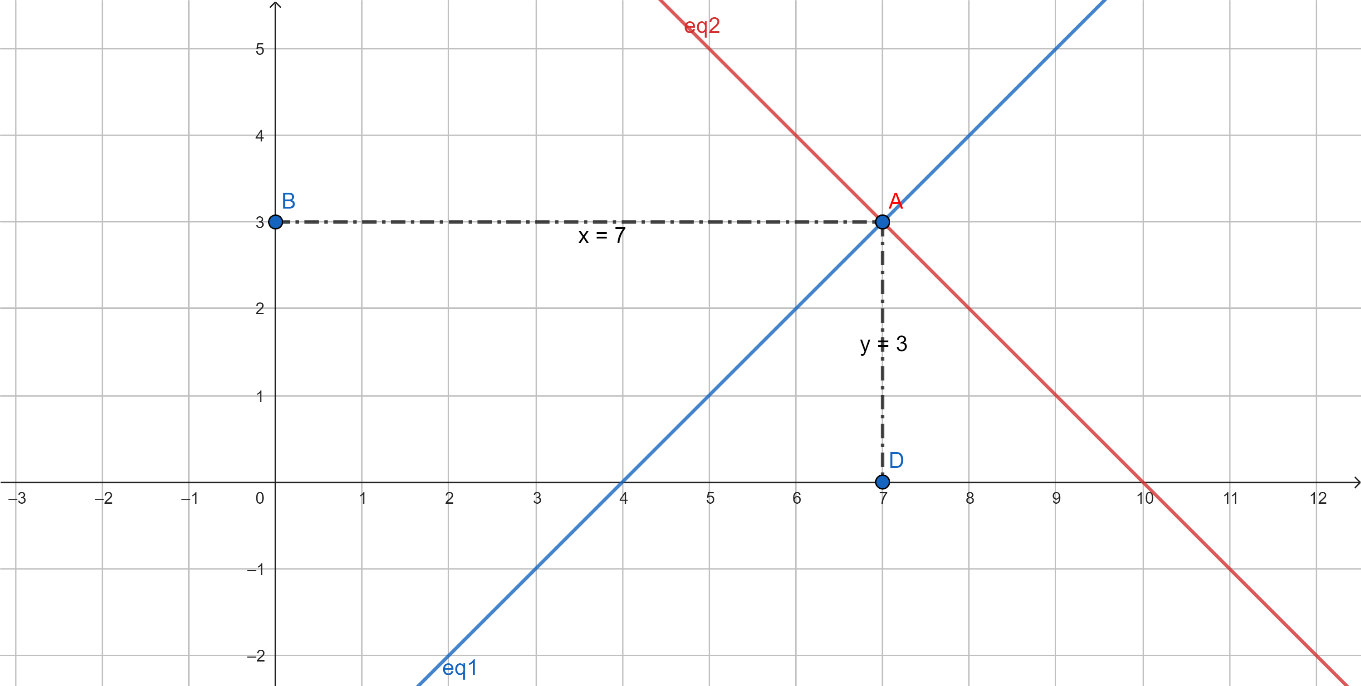
(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
Let,
number of girls = x
number of boys = y
according to question,
𝑥+𝑦=10,
𝑥−𝑦=4
Adding, 2𝑥=14⇒𝑥=7. Hence 𝑦=10−7=3.
Girls=7,Boys=3.
(Graphically, the lines 𝐴(𝑥+𝑦)=10 and 𝑥−𝑦=4 intersect at (7,3).
(
2. On comparing the ratios, , find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
(i) 5x−4y+8=0
7x+6y−9=0
Since , the lines intersect at one point.
(ii) 9x+3y+12=
18x+6y+24=0
Since
All equal lines are coincident (infinitely many solutions).
(iii) 6x−3y+10=0
2x−y+9=0
Since
First two equal, third different parallel (no solution).
3. On comparing the , find out whether the following pairs of linear equations are consistent, or inconsistent:
(i) 3x+2y=5, 2x−3y=7
Since
the lines intersect at one point, so consistent with a unique solution.
(ii) 2x−3y=8, 4x−6y=9
Since
First two equal, third different So, inconsistent (parallel).
(iii)9x−10y=14
Since
the lines intersect at one point so consistent with a unique solution.
(iv)5x−3y=11,10x+6y=−22
Since
All equal consistent, coincident (infinitely many solutions).
(v) 2x+3y=12
Since
All equal consistent, coincident (infinitely many solutions).
4. Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
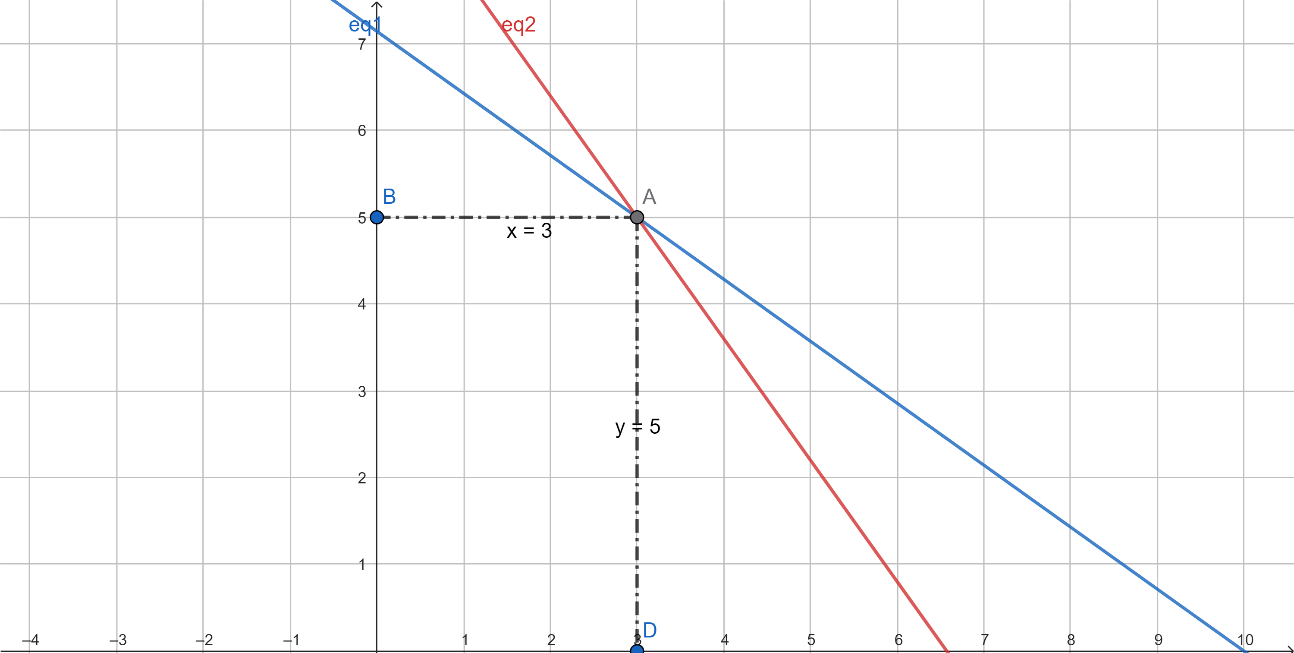
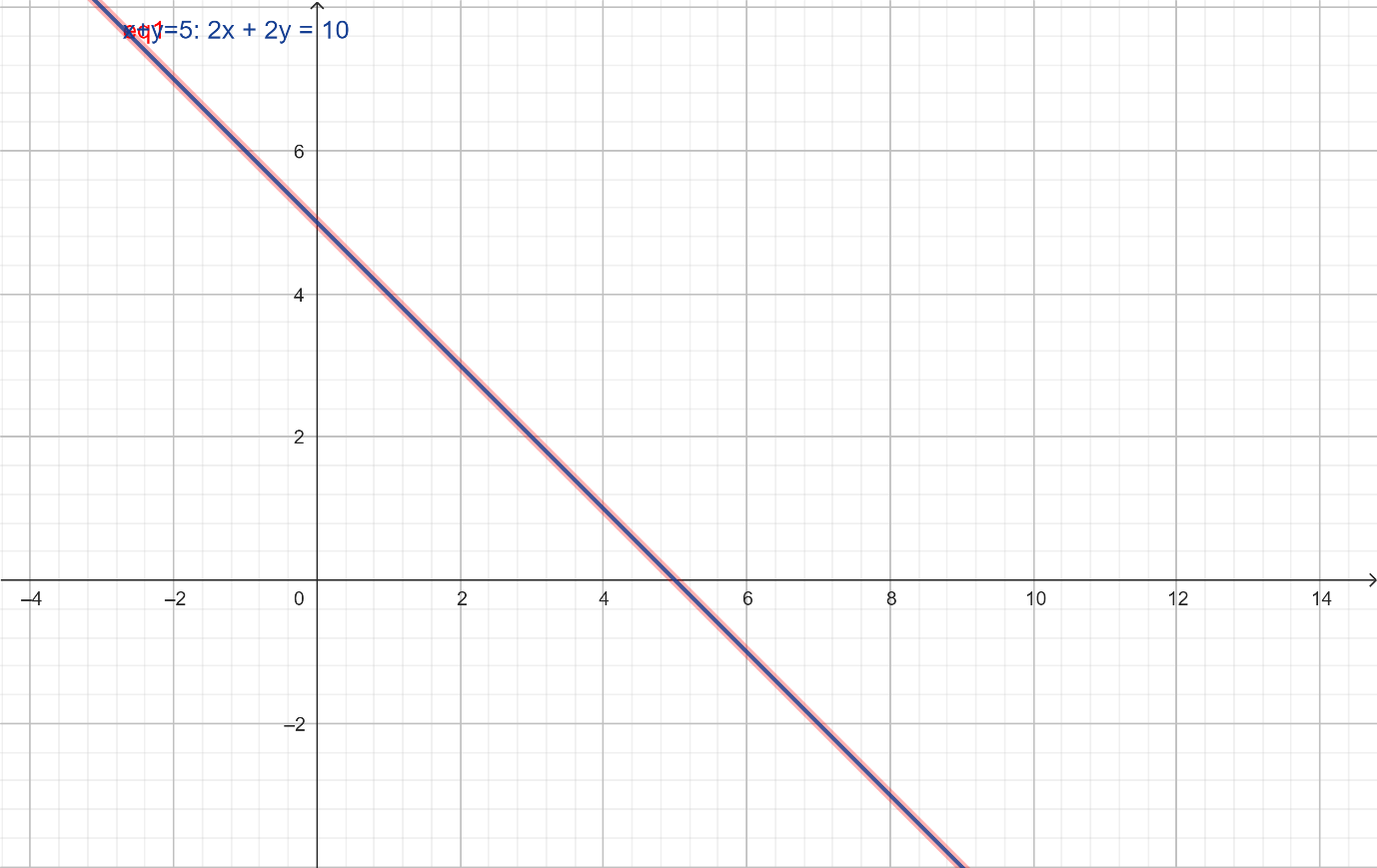
(i) x+y=5, 2x+2y=10
Since
All equal consistent, coincident (infinitely many solutions).
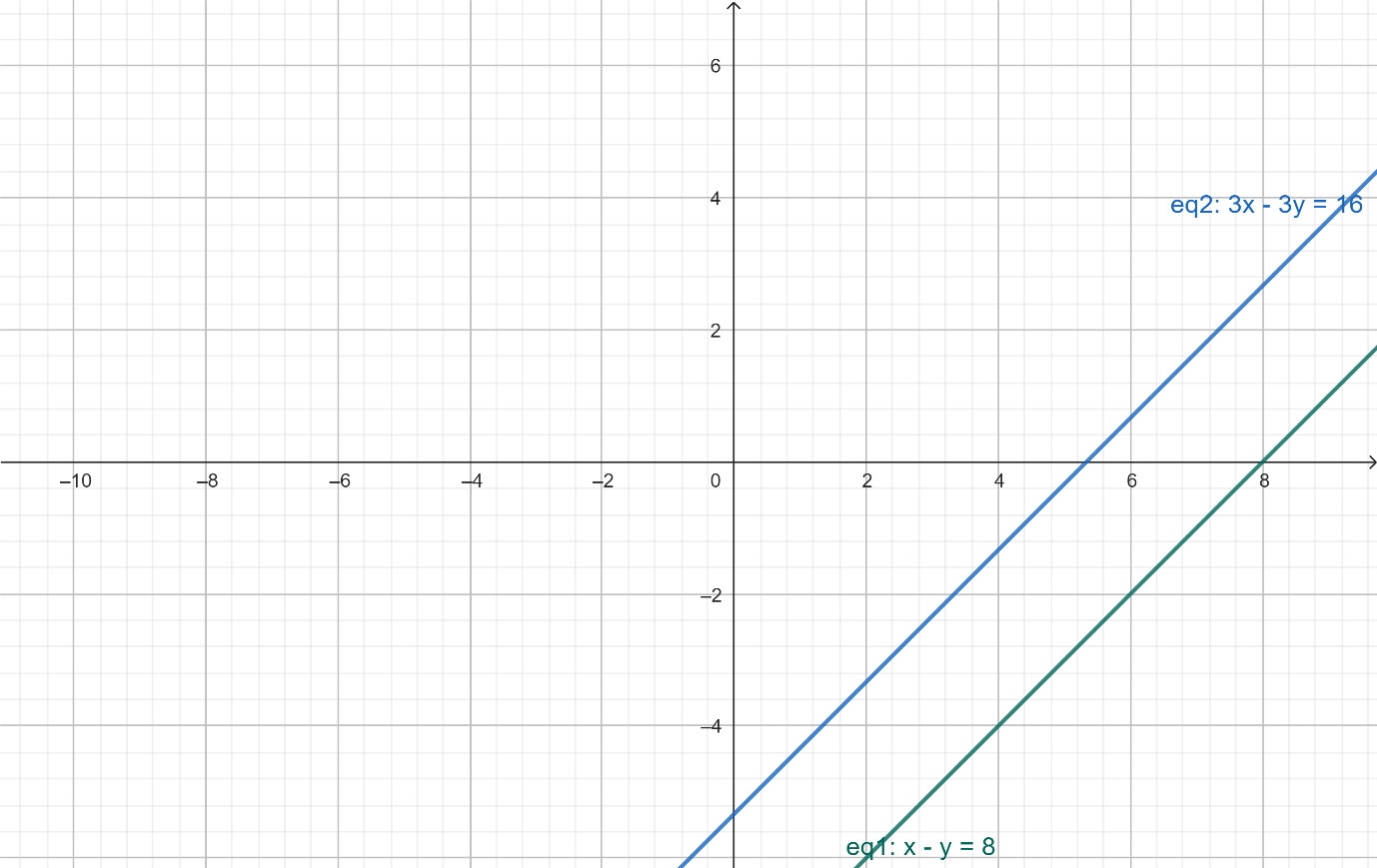
(ii) x−y=8, 3x−3y=16
Since
First two equal, third different So, inconsistent (parallel).
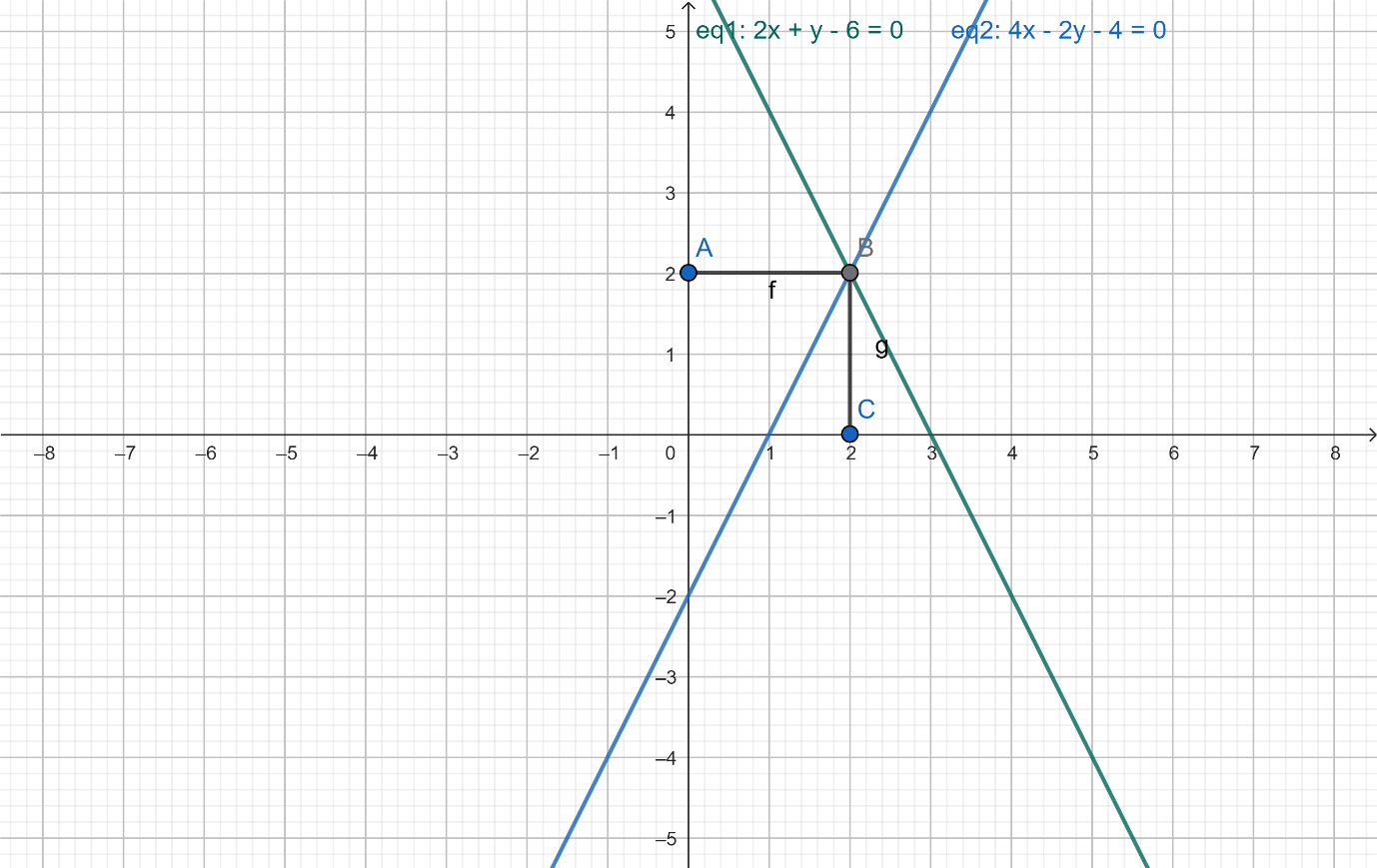
(iii) 2x+y−6=0, 4x−2y−4=0
. Substitute into second:
and hence
Since
the lines intersect at one point so consistent with a unique solution.
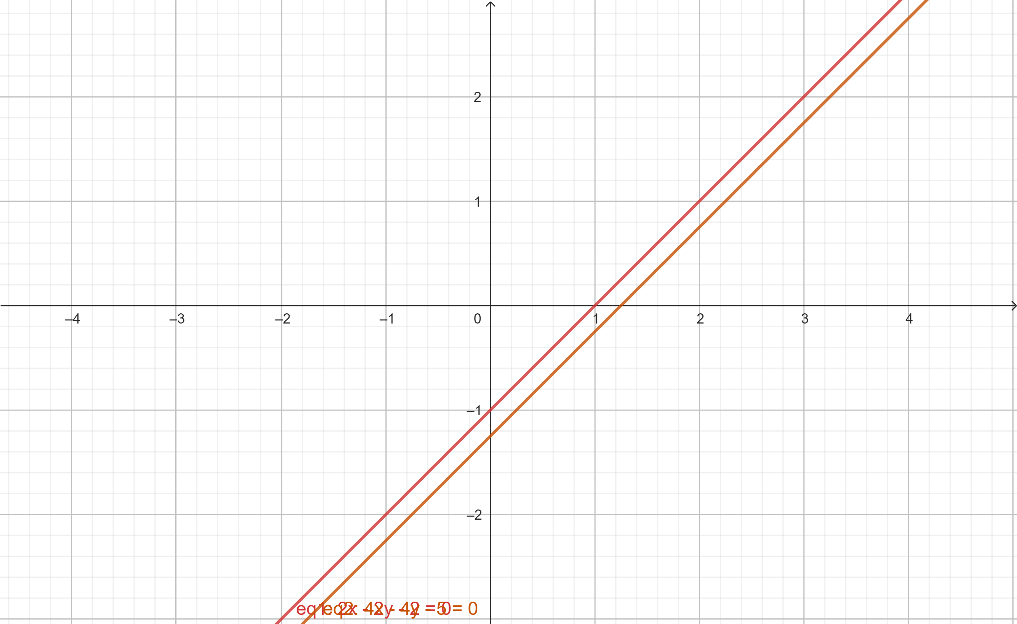
(iv) 2x−2y−2=0, 4x−4y−5=0
Since
First two equal, third different So, inconsistent (parallel).
5. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Let,
width , length . Then
Add: , and .
6. Given the linear equation 2x+3y−8=0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) Intersecting lines
Here,
So for ,intersecting where
Equation 5x+6y-17
(ii) Parallel lines
Here,
So for , Parallel where
Equation
(iii) Coincident lines
Here,
So for , Coincident lines where
Equation
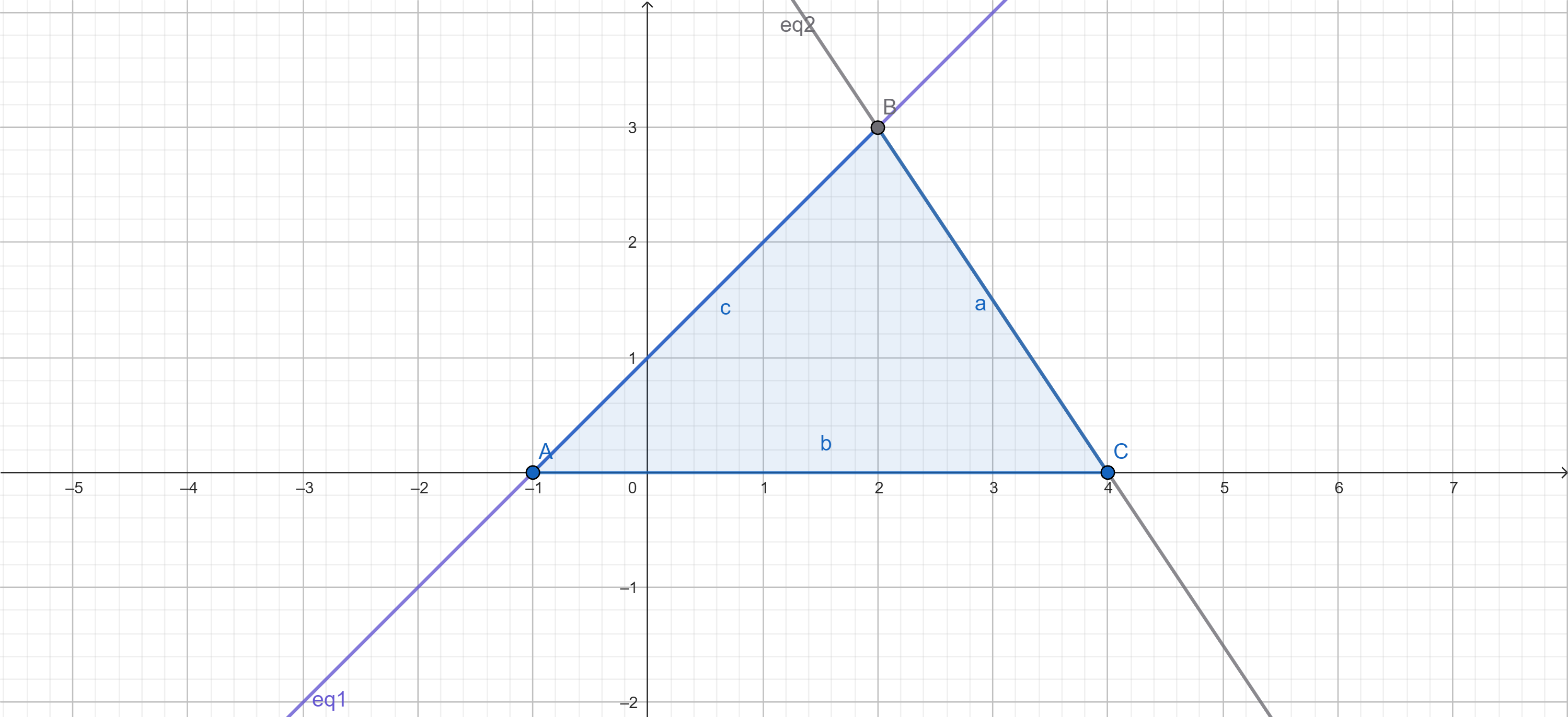
7. Draw the graphs of the equations x−y+1=0and 3x+2y−12=0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.